Chio-chan no Tsuugakuro 12
So I was rewatching Chio-chan no Tsuugakuro, and I got completely nerd-sniped by this geometry problem.
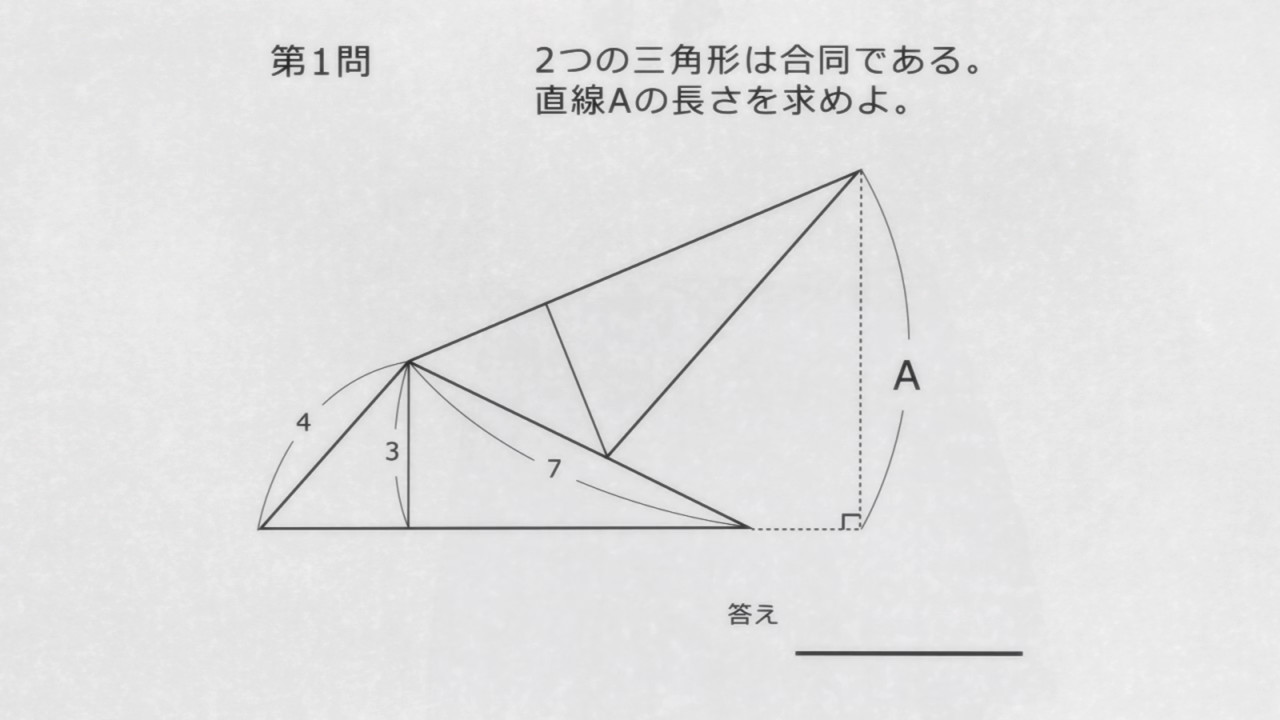
I don’t think my solution is the most elegant, but here it is.
I have made the assumption that the line labelled “3” is parallel to the line labelled “A”. I will also make the notational change to use lowercase “a” instead of uppercase “A” to represent the required length.
Label the points and angles as follows.
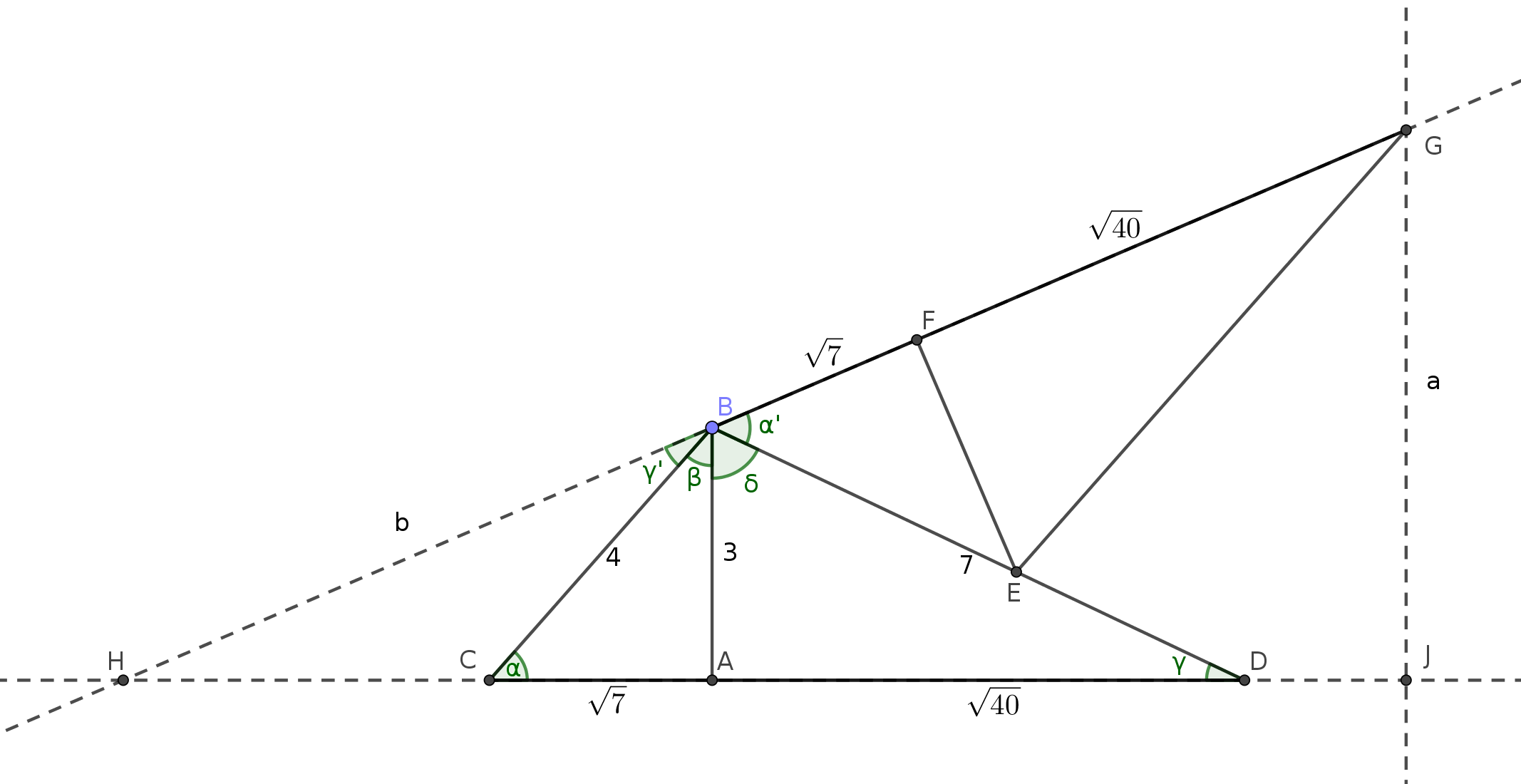
By congruence, \( \alpha = \alpha’ \).
Considering \(\triangle CBD\), \(\alpha + \beta + \gamma + \delta = \pi \); considering straight line HBG, \(\alpha’ + \beta + \gamma’ + \delta = \pi \). Therefore \(\gamma = \gamma’\).
Lengths \(CA\) and \(AD\) are found by Pythagoras’ Theorem, and lengths \(BF\) and \(FG\) by congruence.
Note that \(\triangle HBA \sim \triangle HGJ\), so
\[\frac{b}{b+\sqrt{7}+\sqrt{40}} = \frac{3}{a}\]which gives
\[a = \frac{3}{b} \left(b+\sqrt{40}+\sqrt{7}\right). \tag{1}\]Consider \(\triangle HBA\), we have
\[\cos(\beta+\gamma) = \frac{3}{b},\]so
\[\cos\beta\cos\gamma - \sin\beta\sin\gamma = \frac3b.\]The sines and cosines of \(\beta\) and \(\gamma\) can be obtained by considering \(\triangle ABC\) and \(\triangle ABD\):
\[\frac{3}{4} \cdot \frac{\sqrt{40}}{7} - \frac{\sqrt{7}}{4} \cdot \frac{3}{7} = \frac{3}{b}\]which rearranges to give
\[\frac{3 \left( \sqrt{40}-\sqrt{7} \right)}{28} = \frac3b \tag{2}\]and
\[b = \frac{28\left(\sqrt{40}+\sqrt{7}\right)}{33}. \tag{3}\]Substitute (2) and (3) into (1), we get
\[a = \frac{3 \left( \sqrt{40}-\sqrt{7} \right)}{28} \cdot \frac{61\left(\sqrt{40}+\sqrt{7}\right)}{33} = \frac{183}{28}.\]