Posts

• 2025-09-29 21:14:31 +0100

  Sozai Saishuka no Isekai Ryokouki - 01

  

• 2025-09-20 00:05:15 +0100

  Silent Witch - Chinmoku no Majo no Kakushigoto - 11

  I think this is the first time in anime I see a good chess score sheet.

  

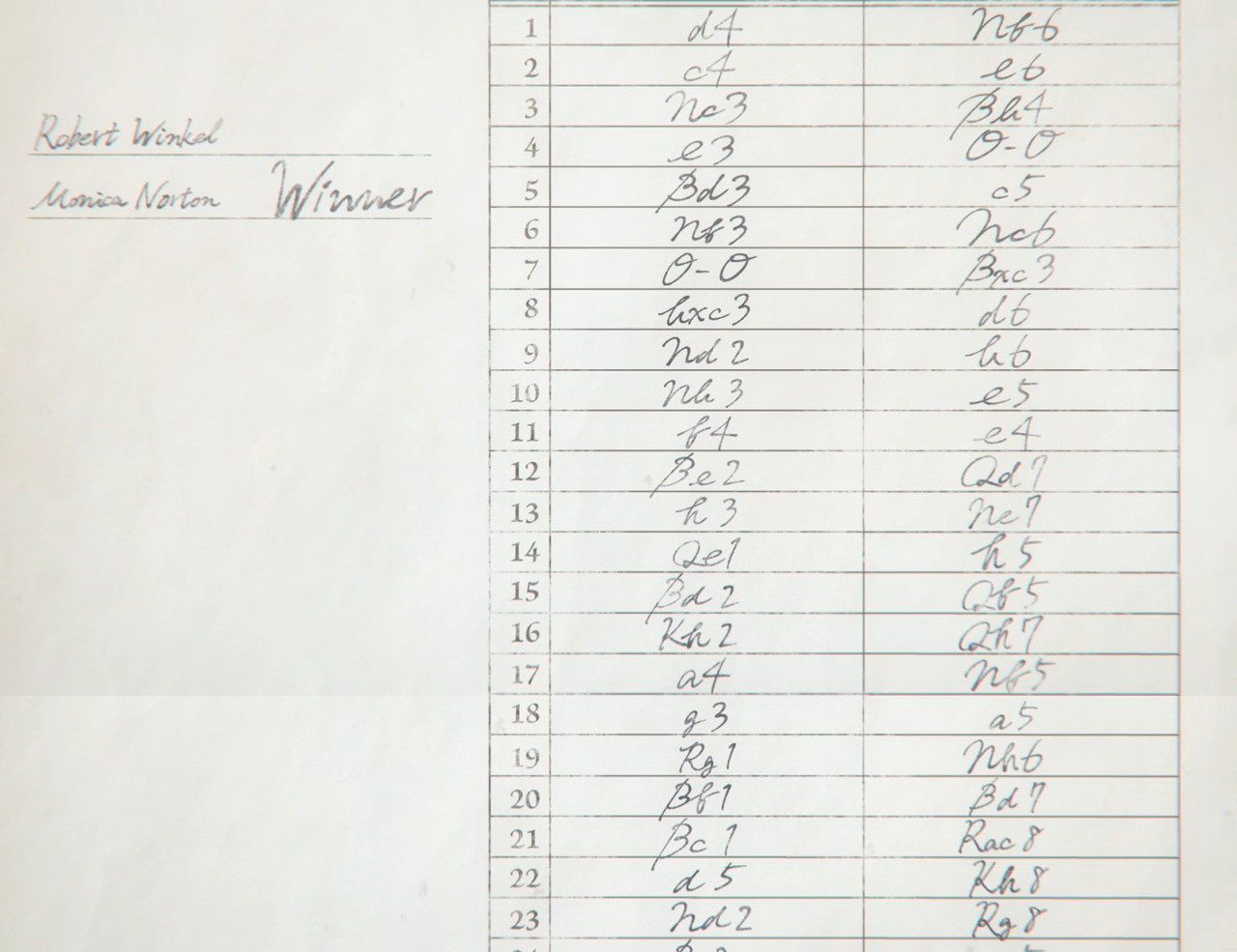
  It’s a shame we didn’t get the full game.

  1. d4 Nf6 2. c4 e6 3. Nc3 Bb4 4. e3 O-O 5. Bd3 c5 6. Nf3 Nc6 7. O-O Bxc3 8. bxc3 d6 9. Nd2 b6 10. Nb3 e5 11. f4 e4 12. Be2 Qd7 13. h3 Ne7 14. Qe1 h5 15. Bd2 Qf5 16. Kh2 Qh7 17. a4 Nf5 18. g3 a5 19. Rg1 Nh6 20. Bf1 Bd7 21. Bc1 Rac8 22. d5 Kh8 23. Nd2 Rg8

  Lichess study: https://lichess.org/study/umb3Fsyi

  ---

  The game just before the ending looks like it could have been an Italian Game.

  

  Assuming it is black to play (because it is black to play after we hear two moves), the FEN is:

  r2qk2r/ppp2ppp/1bnp1n2/4p1Nb/2B1P3/2NPBP2/PPPQ2PP/R3K2R b KQkq - 0 1

• 2025-09-12 00:04:13 +0100

  Mikadono Sanshimai wa Angai, Choroi. - 11

  Another rotated-90-degrees BS.

  

• 2025-08-13 20:51:20 +0100

  Tensei shitara Dainana Ouji Datta node, Kimama ni Majutsu wo Kiwamemasu - 18

  The board is correct in this frame… …but wrong in this frame smh

• 2025-08-03 22:58:00 +0100

  Watari-kun no xx ga Houkai Sunzen - 05 / Seishun Buta Yarou wa Bunny Girl Senpai no Yume wo Minai - 05

  I knew I’ve seen it somewhere!

  

• 2025-08-02 00:34:24 +0100

  Watari-kun no xx ga Houkai Sunzen - 05

  

• 2025-08-01 23:45:35 +0100

  Silent Witch - Chinmoku no Majo no Kakushigoto - 05

  Most accurate chess scene I’ve seen in anime in a long time!

  

  A good start.

  

  Very good start.

  Context: White is a beginner, and black gave queen odds.

  

  This position is:
  r3kr2/p3b3/bpp3p1/1n4Qp/8/1P4N1/P1P2PPP/R1BKR1N1 b q - 0 1

  

  This is correct. The line is:
  1. … O-O-O+ 2. Ke2 Nd4+ 3. Kd2 Ne2+ 4. Ke3 Bxg5+ 5. f4 Bxf4+ 6. Kf2 (6. Ke4 Rde8+ 7. Kf3 Bxg3+ 8. Bf4 Rxf4#) Bxg3+ 7. Ke3 Bf2+ 8. Ke4 Rde8#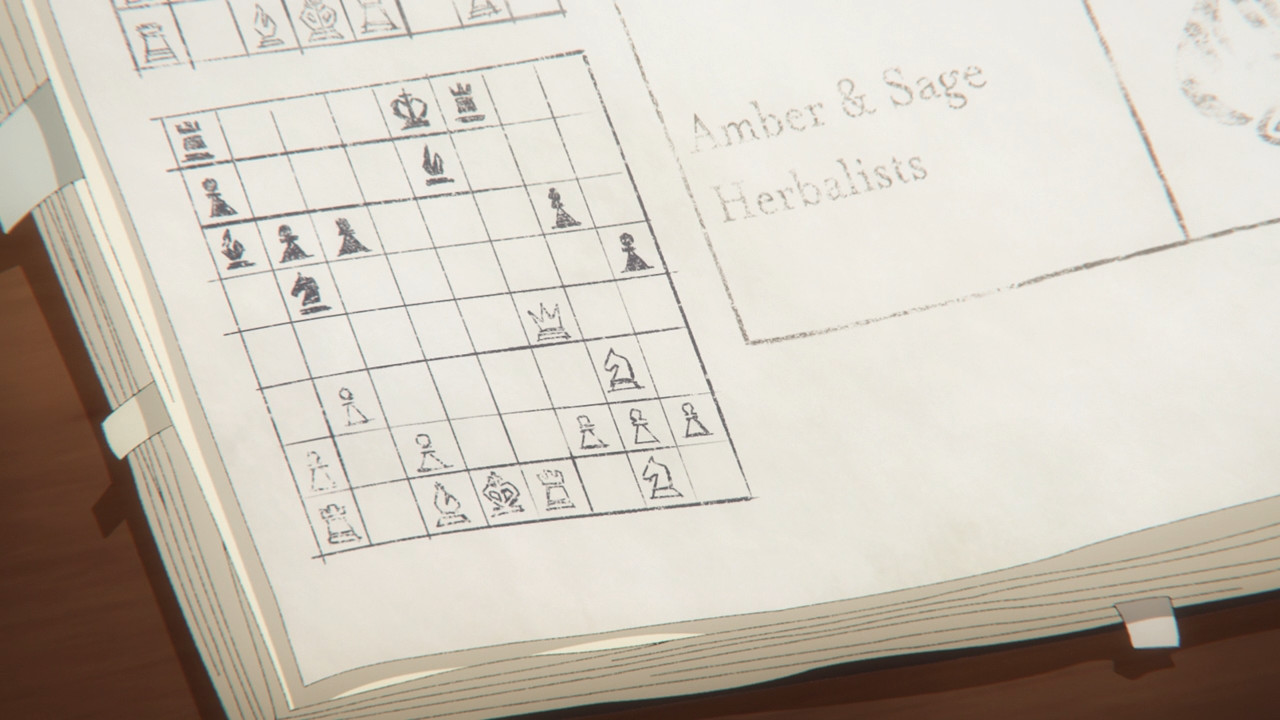

  

  This is presumably one ply before the previous scene, with the queen on f4.

  

  This explains it all. The Japan Chess Federation is credited.

  See? It’s not that hard to make good anime chess scenes!

• 2025-07-29 01:25:49 +0100

  Watashi ga Koibito ni Nareru Wake Nai jan, Muri Muri! (※Muri ja Nakatta!?) - 03

  

  Mixed feelings about this show…

  On one hand, the characters are so hot. On the other hand, the plot is just pure yikes.

• 2025-07-28 20:49:08 +0100

  Grand Blue S2 - 04

  

• 2025-07-26 22:40:40 +0100

  Haite Kudasai, Takamine-san - 12

  

subscribe via RSS